13. NUCLEI (Long Answer Type Question)
Q.1. (i) Find the energy released in the nuclear reaction A = B + C + D the binding energies of A, B, C and EA, EB, EC and ED.
(ii) Nuceli are being added at the rate N nuceli per second in a sample. Its decay constant is λ At t = 0, the number of nuclei is N0. Determine the number at time t.
Ans ⇒ (i) Free energy (mA + mB – mC – mD) C2
Now, E = bound energy of nucleus A = (ZAmp + NAmn – mA)C2 (NA = No. of neutrons is A)
. 
(ii) Number of nucleus added during time dt = ndt and number of disingrated nucleus = -λNdt + dt
Hence no. of reduced nucleus = -dn = -λNdt + ndt
. ![]()
. 
Q.2. Draw a plot showing the variation of binding energy pernuclear with mass mass number A. Write two important conclusions which you can draw this plot. Explain with the help of this plot, the release in energy in the processes of nuclear fusion and fission.
Ans ⇒ The average energy required to release a nucleon from the nucleus is called binding energy per nucleon.
Binding energy per nucleon =
. 
Significance of Binding energy per nucleon :
Binding energy per nucleon determines the stability of a nucleus. That is, stability of a nucleus is proportional to the binding energy/nucleon.

If binding energy per nucleon of a nucleus is less, the nucleus is less stable whereas the nucleus is more stable if its binding energy per nucleon is higher.
The variation of binding energy per nucleon with mass number (A) is shown in the adjoining figure.
From the graph, it is clear that :
(i) For nuclei with mass number A < 20 the binding energy per nucleon increases first rapidly and then gradually till it attains a maximum value 8.8 MeV corresponding to lorn, 26Fe56 nucleus. Thus, Iron is a stable element.
(ii) The peaks in the graph for neclei A < 20 show that some light nuclei are more stable than their neighbours. For example, peaks occur at A = 4, 8, 12, 16 and 20. Thus, 2He4, 4Be8, 6C12, 8O16 and 10Ne20 are most stable than their neighbours.
(iii) For nuclei having A > 56, binding energy per nucleon gradually decreases. For uranium U238, one of the heaviest element, the value of B.E./nucleon drops to 7.5 MeV.
Conclusions : From the above graph, we conclude that.
(i) The binding energy per nucleon has low value for both the light and heavy nuclei. So they are unstable nuclei.
(ii) The intermediate nuclei have large value of binding energy per nucleon, so they are more than the neighbours. This shows that these nuclei are more stable.
(iii) Binding energy per nucleons of light nuclei having mass number A = 4, 8, 12, 16 and 20 is more than the neighbours. This shows that binding energy per nucleon is less for light atoms so energy is released if they combine i.e. when fusion occurs.
The graph also shows that heavy nuclei are unstable so they suffer fission and energy is released thereof.
Q.3. Derive the relation connecting half-life period and decay constant of a radioactive isotope.
Ans ⇒ Let at T = 0, the number of nuclei present be N0. Then the number of nuclei available at t = T, 2T, 3T, etc, is given by
. ![]()
If the time elapsed is not an exact multiple of half life, then we adopt the following method. Let the total number of nuclei present in an element be N. Let dN be the nuclei that will decay in time dt, then dN, is proportional to N and dT i.e.,
dN α NaT; dN = -λNdT …(i)
Here λ is constant, called decay constant. The -ve sign shows that N is decreasing with increase in time. This
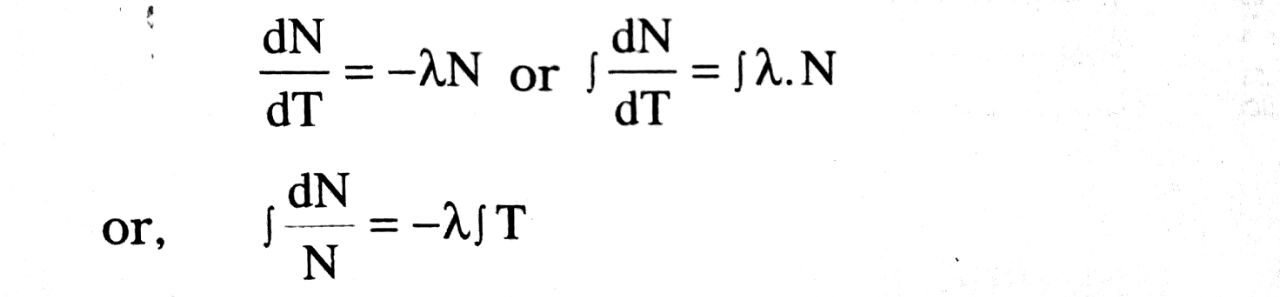
or, log, N = λt + C … (ii)
Where C is constant of proportionality.
When t = 0, N, = N0 hence
logeN0 = C
Putting the value of C in the above equation.
We have,
logeN = -λt + loge N0
. ![]()
. 
The above relation shows that the number of remaining nuclei decreases exponentially with time. Graphi plotted between of remaining atoms and time is shown in figure.
Substituting the value of t = 1/λ in equation N = N0e-λt, we get
. ![]()
Thus decay constant or disintegration constant is the reciprocal of the time. During which the original number of atoms (N0) of a radioactive substance reduces 1/e time the original number of atoms (N0).
Class 12th physics Long Type question in English
| S.N | Physics Long Type Question English Medium |
| 1. | ELECTRIC CHARGES AND FIELDS |
| 2. | LECTROSTATIC POTENTIAL AND CAPACITANCE |
| 3. | CURRENT ELECTRICITY |
| 4. | MOVING CHARGES AND MAGNETISM |
| 5. | MAGNETISM AND MATTER |
| 6. | ELECTROMAGNETIC INDUCTION |
| 7. | ALTERNATING CURRENT |
| 8. | ELECTROMAGNETIC WAVES |
| 9. | RAY OPTICS AND OPTICAL INSTRUMENTS |
| 10. | WAVE OPTICS |
| 11. | DUAL NATURE OF MATTER AND RADIATION |
| 12. | ATOMS |
| 13. | NUCLEI |
| 14. | SEMI CONDUCTOR ELECTRONICS |
| 15. | COMMUNICATION SYSTEMS |
