1. ELECTRIC CHARGES AND FIELDS ( LONG ANSWER TYPE QUESTION )
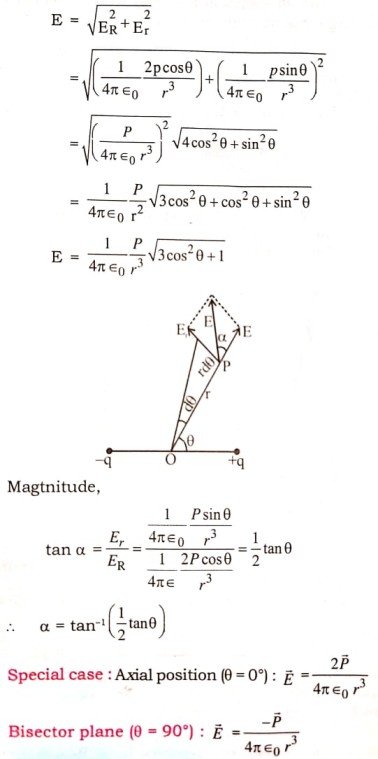
Q.1. Calculate electric potential and intensity a point P (r, θ) due to an electric dipole.
Ans ⇒ Electric potential and field intensity at Point due to electric dipole : Let us consider an electric dipole AB is a system to two charges -q and +q of equal magnitude, but of opposite sign and separated by a distance 21 from each other. Therefore, an electric dipole moment p = 2ql ‘p’ is a point of polar co-ordinates (r,θ) with respect to the axis as the reference line and the mid-point of the dipole 0. Drawn PK ⊥ BG & AK ⊥ OP and its raised portion OP =r, ∠POB = θ 20G = OK 1 cos θ

In broadside onoposition (0 = 90°)→ Vp = 0
Electric field intensity at point due to electric dipole:


Resultant electric field intensity at point p due to electric dipole,
Q.2. What do you understand by an electric dipole ?
Ans ⇒ Electric Dipole : Two point charges of opposite sign and the same magnitude, separated by a small distance between them, constitute an electric dipole.
In the figure, q and -q are separated by 2a.
This system is an slectric dipole. The electric field of an electric dipole is described busing a quantity P = 2 aq called dipole moment.
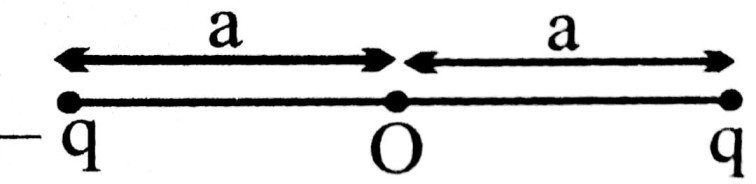
Authough an electric dipole is neutral, its electric field is not Zero because its two charges are non coincident.
Q.3.Find expression for work done in rotating an electric dipole in uniform electric field.
Ans ⇒ We consider an electric dipole whose each charge is of magnitude q & length of dipole is 2l.
AB = 2l.
Torque (τ) = F x q.2l sinθ = pE sinθ, Where = 2ql.
If dipole is rotated by an angle dθ them work done dW = τ.dθ
So work done in rotating dipole from θ1 to θ2 is

or, W = +pE[+cosθ1 – cosθ2] if, θ1 = 0° & θ2 = θ
then W = pE(1-cosθ)
This is required expression.

If θ = 0° then W = 0, if θ = 180° then W = 2 pE, if θ = 90° then W = pE.
Q.4. Obtain on expression for the torque acting on an electric dipole suspended freely in a uniform electric field.
Ans ⇒ Torque on an electric dipole :
Let us consider an electric dipole AB whose unlike charge + qand – q are at very small distance 2l. The dipole is suspended freely in a uniform electric field ![]()

If the dipole, the deflected from the directioin of ![]() by on angle θ, the force ( q
by on angle θ, the force ( q![]() ,q
,q![]() )
)
acting on the charges are equal, opposite and parallel and constitute a couple. This couple tries to bring the dipole in the direction of ![]() hence it is called restering or controlling couple. The moment of this couple or torque is
hence it is called restering or controlling couple. The moment of this couple or torque is
τ = force x force arm
= qE (AP)
= qE x 2l cosθ
= (q.2l) x E cosθ
= p E cosθ …(1)
where p = q.2l
= dipole moment
![]() and
and ![]() are vectors, so in vector rotation.
are vectors, so in vector rotation.![]()
Q.5. Define electric intensity. Derive an expression for electric intensity at a point on (a) the axis of electric dipole and (b) the equatorial position.
Ans ⇒ Electric Intensity : Electric intensity at a point in an electric field is defined as the force acting on a unit test charge placed at that point. The electric intensity at a point placed at a distance r from a charge + q is given by
![]()
It is a vector quantity and its SI unit is (NC-1) or (Vm-1).
(a) Electric intensity due to an electric dipole in axial position :


Q.6. Using Gauss’s theorem, show mathematically that for any point outside the shell, the field due to a uniformly charged thin spherical shell is the same as if the entire charge of the shell is concetrated at the centre. Why do you expect the electric field inside the shell the zero according to this theorem ?
Ans ⇒ Gauss theorem : This theorem relates the total charge inside a closed region to total flux associated with the surface. According to this theorem total electric flux associated with a closed surface is 1/ε0 times total charge inside the region ![]()
Gauss’s law & Coulomb’s law are equivalent. They can be obtained from each other.
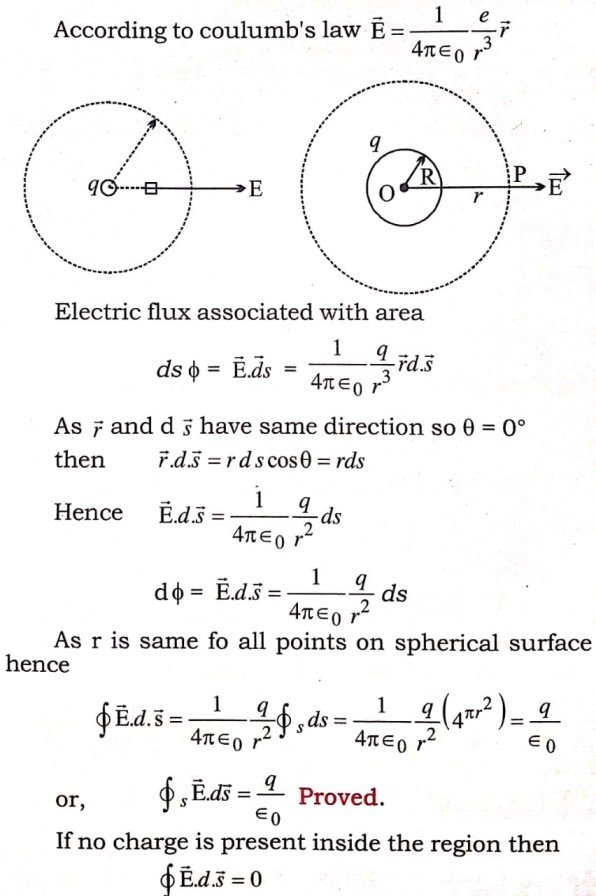
Application : (i) Intensity at a point due to a point charge the electric field intensity at each point due to a point charge is radial. Intensity at all points equidistant from a point charge are equal. We imagine a Gaussian surface.
Gauss’s law
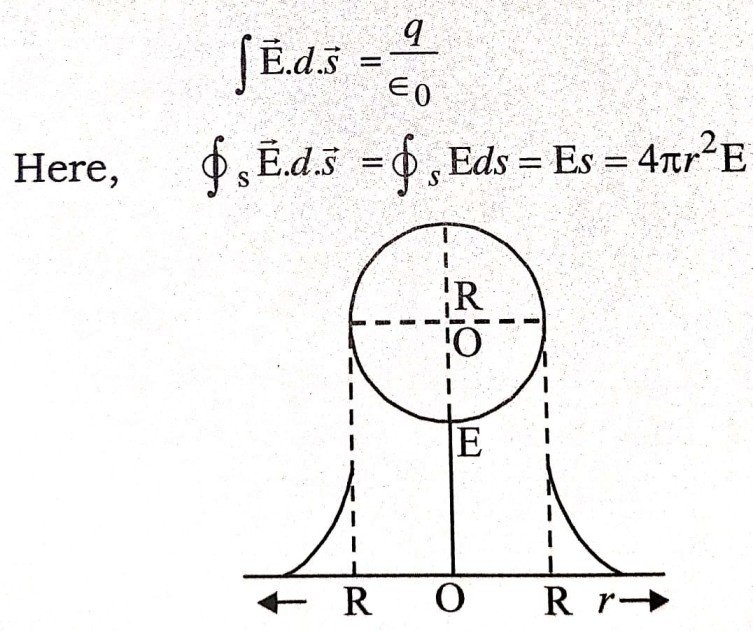

Here charge q is situated insided the sphere of radius r. The intensity inside a hollow spherlal charged conductor is zero.
Class 12th physics Long Type question in English
| S.N | Physics Long Type Question English Medium |
| 1. | ELECTRIC CHARGES AND FIELDS |
| 2. | LECTROSTATIC POTENTIAL AND CAPACITANCE |
| 3. | CURRENT ELECTRICITY |
| 4. | MOVING CHARGES AND MAGNETISM |
| 5. | MAGNETISM AND MATTER |
| 6. | ELECTROMAGNETIC INDUCTION |
| 7. | ALTERNATING CURRENT |
| 8. | ELECTROMAGNETIC WAVES |
| 9. | RAY OPTICS AND OPTICAL INSTRUMENTS |
| 10. | WAVE OPTICS |
| 11. | DUAL NATURE OF MATTER AND RADIATION |
| 12. | ATOMS |
| 13. | NUCLEI |
| 14. | SEMI CONDUCTOR ELECTRONICS |
| 15. | COMMUNICATION SYSTEMS |
