Q.1. State and explain Biot-Savart Law. Find an expression for magnetic induction at a sistance from a straight wire of infinite length.
Ans ⇒ Biot-Savart Law : Biot Savart law gives an expression for magnetic induction ![]() at a point positioned
at a point positioned ![]() relative to a current
relative to a current ![]() as its source. În vector form, the law may be written as
as its source. În vector form, the law may be written as
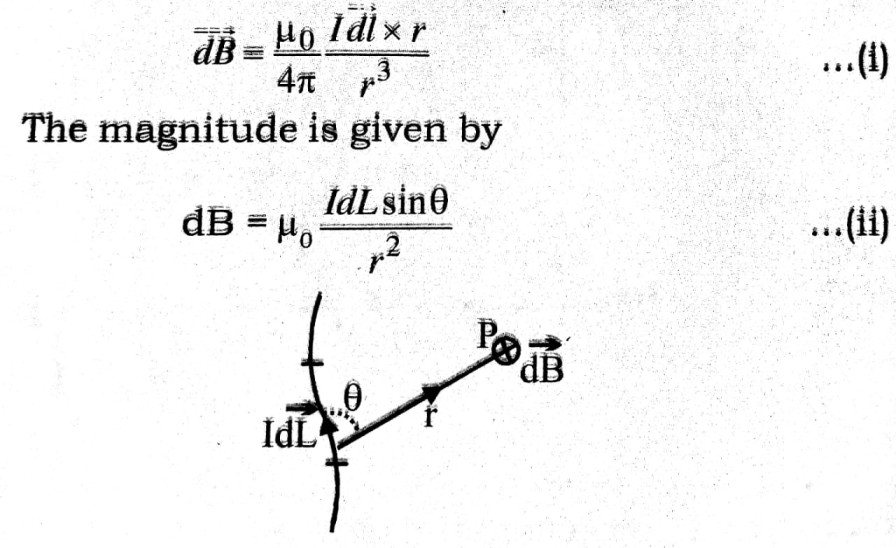
In the figure, the position vector of a point p relative to current element ![]() The magnetic induction at P will have a direction along
The magnetic induction at P will have a direction along ![]() and magnitude porportional to Idl sinθ and inversely proportional to r2. Both these results are expressed in vector form in equation (i)
and magnitude porportional to Idl sinθ and inversely proportional to r2. Both these results are expressed in vector form in equation (i)
![]() due to infinite wire : If we sprinkle iron filings around a current carrying wire ofinfinite length, they are arranged in circles. The direction of
due to infinite wire : If we sprinkle iron filings around a current carrying wire ofinfinite length, they are arranged in circles. The direction of ![]() is tangential to these circles.
is tangential to these circles.
Let a point P be at a dicxtance r from the wire. Computing line integral of

Q.2. Obtain expression for B due to a circular current. Find expression for torque on current loop.
Ans ⇒ When a current of strenth i flows through a closed circuit; magnetic force field at a point is due to current in total circuit. But for shake of convenience total circuit is divided into many elementry protions. In each elementory portion current is i, then ids is called current element. Magnetic force field due to current element in vacuüm or air is given by,
![]()
This expression for magnetic force field due to current element is mathematical form of Biot-Savart Law. This also gives laplace’s law.
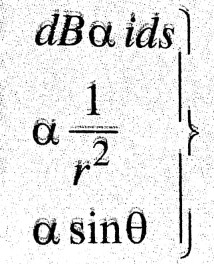
i.e, magnetic from field due to current element is proportional to the current element, angle sinθ & inversely proportional to the square of distance at the point from current element. Biot-Savärt law and Laplace’s law are based on experiemental facts.
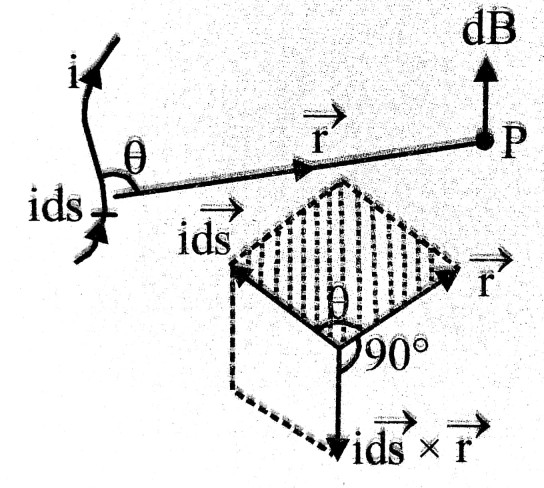
Magnetic force field along axis of current carrying circular coil : Let us consider and element L’M’opposite to LM having same length δl. Magnetic force field due to L’M’ at point P has same magnitude Δ B, But its direction will be alsog PR’. The componets along axis & ⊥ to axis are Δ B sin φ & Δ B cos φ. So resultant force field along OP = Δ B sin φ + Δ B sin φ = 2 Δ B sin φ.
Resultant field ⊥ OP = Δ B cos φ – Δ B cos φ = 0
i.e, resultant force field due to all components will be along OP.
Torque on a current loop placed in magnetic field : Let there be a rectangular loop PQRS which is suspended between pole pieces N & S of a strong magnet. The magnetic field is B.
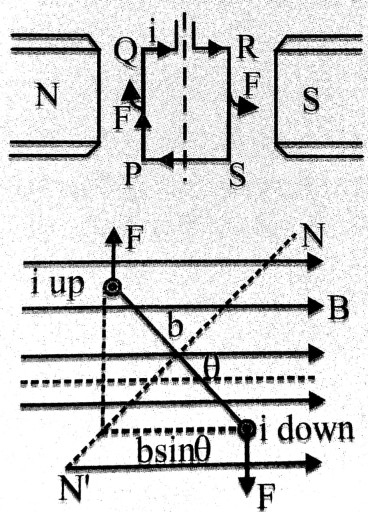
Length of loop is PQ = RS = l and breadth is QR = SP = b. If strenth of current flowing in loop is l then a force acts on coll carrying curent placed in a magnetic field. The current loop will experience a force on its each arm. Its direction is given by Fleming left hand rule. Let axis of current loop makes an angle with direction of magnetic force field (B).
So torque acting on current loop is given by
τ = F x ⊥ distance = BIl x b sin θ = IBl x bsin =
| ∴ τ = BIAsinθ |
Here, A = l x b & I → strength of current.
If θ = 0° then τ = BIA sin 0° = 0
i.e. in this situation τ = 0
Q.3. What is a cyclotron ? Explain its working with the help of a diagram.
Ans ⇒ Cyclotron Is a particle accelerator, In cyclotron, energy is imparted to the charged particle by electric field and magnetic field makes the charges turn round and round in the electric field so that it can pick up energy, The accelerator is based on motion of charged particles in electric and magnetic fields.

Action: A cyclotron is schematically shown in the figure. Source of particles sends charged particle in D-type vessel D2. A perpendicular magnetic field ![]() exerts a force
exerts a force ![]()
In the D-vessel. It circulates the particle, Moving half of a circle in D2, the particle enters the gap where electric field ‘accelerates’ it by a force ![]()
The speed is increased and hence the radius also increases as ![]() the particle enters with increased speed and radius. As the periodic time T
the particle enters with increased speed and radius. As the periodic time T ![]() is independent of speed, it competes half circle in D1 and enters the gap. In the mean time, Ē in the gap has reversed direction and thus accelerates the particle to higher speed, In this way the particle accelerates and gains kinetic energy, At the end, it is deflected by deflectors and thrown out with high speed.
is independent of speed, it competes half circle in D1 and enters the gap. In the mean time, Ē in the gap has reversed direction and thus accelerates the particle to higher speed, In this way the particle accelerates and gains kinetic energy, At the end, it is deflected by deflectors and thrown out with high speed.
If the final radius of its path be R, R = mv/qB

The particle comes out of the cycotron with this kinetic energy. The cyclotron is thus a particle accelerator.
Q.4. What is shunt ? Derive explression for the current passing through the galvenometer and the shunt. Mention Universal shunt.
Ans ⇒ Shunt : Shunt is a low resistance wire connected prallel to a galnernometer to save it from the strong current of the circuit.
Let G and S be the reristance of the galvenometer and the shunt and I, Ig, Is be the main current, current through the galvenometer and the shunt respectively.
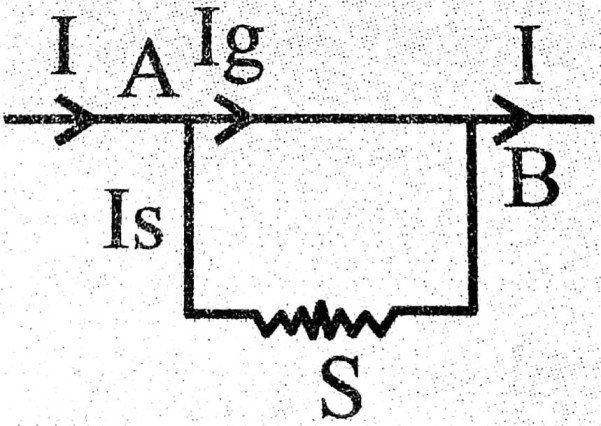
From kirchoffs point rule for point A or B,
I = Ig + Is …(1)
From Ohm’s law for galvenometer circuit
Ig . G = V
For shunt circuit –
Is. S = V
Where V is the potential difference between points A and B.

Universal Shunt : It is a series of resistance connected parallel to galvenometer so that
1/100th or 1/100th times the main current is passed through the galvenometer by changing the rocker only.
Class 12th physics Long Type question in English
| S.N | Physics Long Type Question English Medium |
| 1. | ELECTRIC CHARGES AND FIELDS |
| 2. | LECTROSTATIC POTENTIAL AND CAPACITANCE |
| 3. | CURRENT ELECTRICITY |
| 4. | MOVING CHARGES AND MAGNETISM |
| 5. | MAGNETISM AND MATTER |
| 6. | ELECTROMAGNETIC INDUCTION |
| 7. | ALTERNATING CURRENT |
| 8. | ELECTROMAGNETIC WAVES |
| 9. | RAY OPTICS AND OPTICAL INSTRUMENTS |
| 10. | WAVE OPTICS |
| 11. | DUAL NATURE OF MATTER AND RADIATION |
| 12. | ATOMS |
| 13. | NUCLEI |
| 14. | SEMI CONDUCTOR ELECTRONICS |
| 15. | COMMUNICATION SYSTEMS |

