9. RAY OPTICS AND OPTICAL INSTRUMENTS
Q.1. What is total internal reflection ? Explain its two applications.
Ans ⇒ Total internal reflection : Consider the incident ray I1 which retracts as R1. When the angle of incidence is increased to ie the incident ray I2 refracts as R and glaze the surface. When angle of incidence is increased beyond the value of ie the complete light comes back to the same medium and phenomenon is called total internal reflection. Ie, total internal reflection i, the angle of incidence for which angle of refraction becomes 90° is called critical angle.
∴ For total internal reflection (i) the angle of incidence must be greater than critical angle and (ii) Light should pass from denser medium to the rarer medium.
For the light passing from water
. ![]()

where μ is the refractive index of the medium with respect to free space.
Applications of total internal reflection :
(i) Mirage : The atmosphere can be considered as made up of layers of air. The atmosphere gets heat from sun directly through radiation. Therefore the air in the contact of the surface of earth remains more warmer as the upper layers of air in atmosphere. Due to this variation of temperature, the density of upper layers of air remains more than the density of lower layers of air. When light passes through the atmosphere the angle of incidence at each layer of air increases and for certain layer becomes greater than the critical angle and total internal reflection takes place due to which an inverted image of the object is forrned just below the object as through reflected from pool of water and gives an illusion of presence of water.
Thus, mirage is the phenomenon of optical illusion based upon the principle of total internal reflection. It is very common in hot countries and in deserts.
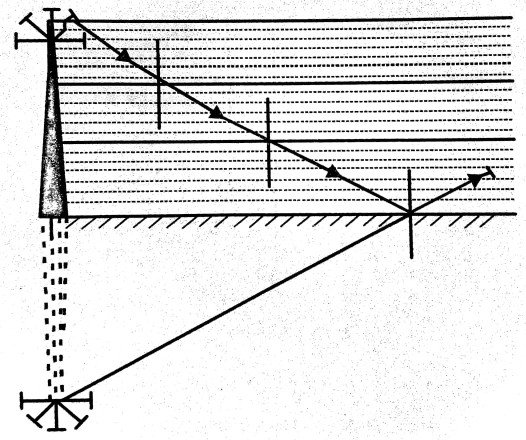
(ii) Optical fibres : Optical fibres consists of a pipe of very small diameter (incident of μ m) of thousands of long and extremely thin strands lower refractive index. When light falls at a small angle at one end of the optical fibre, it gets refracted into the core and incident on the corecladding interface. The angle of incident at the interface is more than the critical angle and total internal reflection takes place. Therefore in optical fibres, the light energy is passed from one end to another without much loss of energy. Now a days optical fibres have great use in (i) Endoscopy, (ii) Transmission of electromagnetic signals and (iii) Telephone cables etc.

Q.2. With the help of a ray diagram, show the formation of image of a point object by refraction of light at a spherical surface separating two media of refractive indices n1 and (n2 > n1) respectively. Using this diagram derive the relation.
![]() Write the sign conventions used. What happens to the focal length of convex lens when it is immersed in water ?
Write the sign conventions used. What happens to the focal length of convex lens when it is immersed in water ?
Ans ⇒ In Fig. XY is convex refracting surface separating media 1 and 2.0 is a point object on the principal axis. OA is an incident ray which is refracted along AL ‘i’ is the angle of incidence and r is the angle of refraction. Another ray OP strikes normally and goes without any deviation. The two rays meet at I, so I is the image of O.
Lef ∠AOP = α, ∠AIP = β and ∠ACP = r
From Snell’s law
. 
or, n1 sini = n2 sinr
As angles i and r are small, we have
sin i = i
sin r = r
n1i = n2r …(i)
Now, in ΔOAC, ΔOAN is external angle of ΔOAC
So, i = d + r … (ii)
Similarly, in ΔACI,
r = r + β;
or, r = γ – B … (iii)
Putting the values of i and r from equations (ii) and (iii) in equation (i), we have
n1(α + γ) = n2(α – β) …(iv)
For small aperture of the refractive surface, we have

Q.3. Derive an expression for refractive index of the material of a prism.
Ans ⇒ The figure shows a prism of angle A and refractive index of its material y, placed in air.

i = angle of incidence
i’= angle of emergence
r = refraction angle at Q
r’= incidence angle at R
For refraction at the first face AB,
sin i = μ sin r …(i)
For the refraction at the second face AC,
μ sin r’ = sin i’
The deviation produced by the prism is given by
δ = (i – r) + (i’ – r’) = (i + 1′) – (r + r’)
From geometry of figure,
. 
The graph of δ against i is of the nature shown in the figure. For a general δ, i and i’ are two angles for the same δ. For the minimum value δm, of δ,i = i’. The ray is passing symmetrically through the prism, Then, from (i) and (ii), r = r. These give (equation (iii))

Q.4. Describe the construction and action of a compound microscope and obtain expression for its magnifying power.
Ans ⇒ Compound microscope : Compound microscope is such an optical instrument with the help of which tiny objects are seen clearly.
In this instrument there are two convex lens which are set co-axially in tube. The lens facing the object is called object lens and lens facing the eye called eye lens. The focal length and aperture of objective lens is smaller than eye lens. There is an arrangement of moving eye lens back and forth.
When object is placed before objective its real, inverted and magnified image is formed. Now eye lens is so adjusted that this image lies within the focus of eye piece. So final image is formed at least distance of distinct vision.
Magnifying power :


Q.5. Explain the construction and working of an astron mical teliscope. Derive an expression for its magnifying power when the finel image is formed at infinity.
Ans ⇒ Magnifying Power (Angular Magnification) of Astronomical Teliscope : It is defined as the ratio of the angle subtended by the image at the eye when it is a distance of distinct vision to the angle subtended by the object at the eye.


When the final image formed is at infinity, the telescope is said to be in normal adjustment.
The position of the eye piece is adjusted in a way that the final image of the object is virtual, inverted and highly magnified as shown in figure.

In this case, the length of the telescope,
L = C1A’ + A’C2 = f0 + fe …(vii)
Q.6. Describe the defects of vision & their remedy.
Ans ⇒ Defects of Vision : Following are main defects :
(i) Myopia (Short sightedness) : In this case distant objects are not clearly seen i.e., far point is at a distance lesser than infinity so image of distan object is formed before retina

This defect is remoted by using spectacle having divergent (concave) lens (negative power).

(iii) Hypermetropia (Long sightedness) : in this case near objects are not clearly seen i.e., near point is at a distance greater than 25 cm and so image of near object is formed behind the retina.

This defect is cured by the use of spectacle having convergent (convex) lens (+ve focial length & power). it forms the image of near object at the near point of the person.
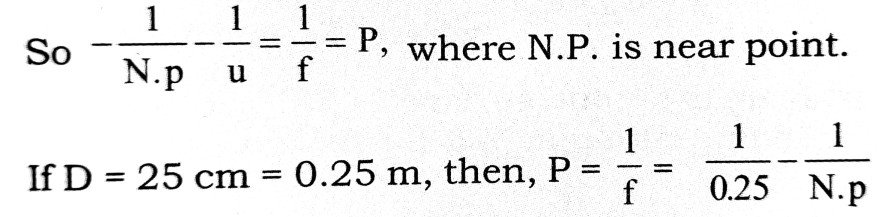
(iii) Persbyopia : In this case far & near both objects are not clearly seen i.e., far point is lesser than infinity and near point grater than 25cm. This is removed by case of bifocal lens. it is an old eleasticity and so can not change the focal length. Eyes lose their power of accodation
(iv) Astigmatism : In this case due to imperfect spherical nature of eye lens, the focial length of eye lens is two orthogonal directions because different and so eyes are unable to see objects in two orthogonal direction clearly.
This defect is directional and is removed by using cylinderical lens is particular direction.
If person is also suffering from long sightedness & short sightedness also then spherocylinderical lens is used.
Q.7. Establish Lens Maker’s formula ![]() where the symbols have their used mentions.
where the symbols have their used mentions.
Ans ⇒ Lens maker’s formula (Proof) : In case of image formation by a lens, the incident ray is refrected twice, at first and second surface respectively. The image formed by first object acts as an object for the second. We use the formula for refraction through spherical surface.

index of medium and lens, R is radius of curvature of spherical surface, u is object distance and u is image distance.
Let us first consider through first surface

Q.8. An equiconves lens of curvature radius r is placed on a horizontal plane mirror. A pin at distance a above it conincides with its image, New a liquid is poured between the lens and the mirror. The pin is now babove the system for image to coincide.
Ans ⇒ From first information f0 cm distance is a
![]()

Q.9. Define dispersive power. Obtain the condition of (a) deviation without dispersion or (b) dispersion without derivation.
Ans ⇒ Dispersive Power : The ratio of agle of dispersion 0 and the deviation of mean yellow ray dy is known as dispersive power of a prism.

(a) Condition of deviation without dispersion : For getting deviation without dispersion a pair of crown glass prism and flint glass prism are placed together in such a manner that their angles of prism A and A’ respective are opposite to each other. Let the regractive incdices of crown glass for violet, yellow and red rays are
μv, μy and μr and of the same rays the refractive indices of flint glass are μv’, μy and μr’. The dispersive powers of crown glass prism and flint glass prism are ω and ω’ respectively

The dispersion produced by crown glass prism δv – δr = (μv – μr) A. The dispersion produced by flant glass prism δv’ – δr’ = (μv’ – μr’) A’.
For null dispersion, the total dispersion by the two prism = 0.

This is the required condition of deviation without dispersion. The negativesign indicates that A and A’ are in opposite direction.
The total deviation in this condition is
. 
. 
Condition of dispersion without deviation : The deviation produced by crown glass prism δc = (μy – 1)A. The deviation produced by Flint glass prism, δF = (μy’ – 1)A’.
. 
This is the required condition of dispersion without deviation. The negative sign indicates that A and A’ are opposite to each other.
The total dispersion in this condition is

Q.10. Derive an expression for the focal length of an equivalent lens of two thin lenses separated at a distance.
Ans ⇒ Two thin lenses are placed coaxially at a separation. The incident ray AB and the emergent ray CD intersect at E. The perpendicular from P to the principal axis falls at P. The equivalent lens should be placed at this position P. A ray ABE going parallel
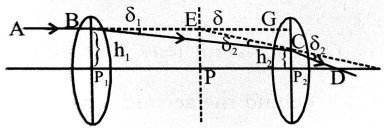
to the principal axis will go through the equivalent lens and emerge along ECD. The angle of deviation is

Class 12th physics Long Type question in English
| S.N | Physics Long Type Question English Medium |
| 1. | ELECTRIC CHARGES AND FIELDS |
| 2. | LECTROSTATIC POTENTIAL AND CAPACITANCE |
| 3. | CURRENT ELECTRICITY |
| 4. | MOVING CHARGES AND MAGNETISM |
| 5. | MAGNETISM AND MATTER |
| 6. | ELECTROMAGNETIC INDUCTION |
| 7. | ALTERNATING CURRENT |
| 8. | ELECTROMAGNETIC WAVES |
| 9. | RAY OPTICS AND OPTICAL INSTRUMENTS |
| 10. | WAVE OPTICS |
| 11. | DUAL NATURE OF MATTER AND RADIATION |
| 12. | ATOMS |
| 13. | NUCLEI |
| 14. | SEMI CONDUCTOR ELECTRONICS |
| 15. | COMMUNICATION SYSTEMS |

