1. SOLID STATE LONG ANSWER TYPE QUESTIONS
1. SOLID STATE – LONG ANSWER TYPE QUESTIONS
Q. 1. How can you determine the atomic mass of an unknown metal if you know its density and The dimension of its unit cell ? Explain.
Ans ⇒ Let ‘a’ be the edge length of a cubic unit cell and it contains ‘Z’ atoms of a substance of atomic mass ‘M’.
Mass of unit cell = No. of atoms in unit cell x mass of each atom = Z × M where M is mass of one atom
= ![]() =
= ![]() (NA is Avogrado’s number)
(NA is Avogrado’s number)
Volume of unit cell = a
Denasity of unit cell = ![]()
Density, 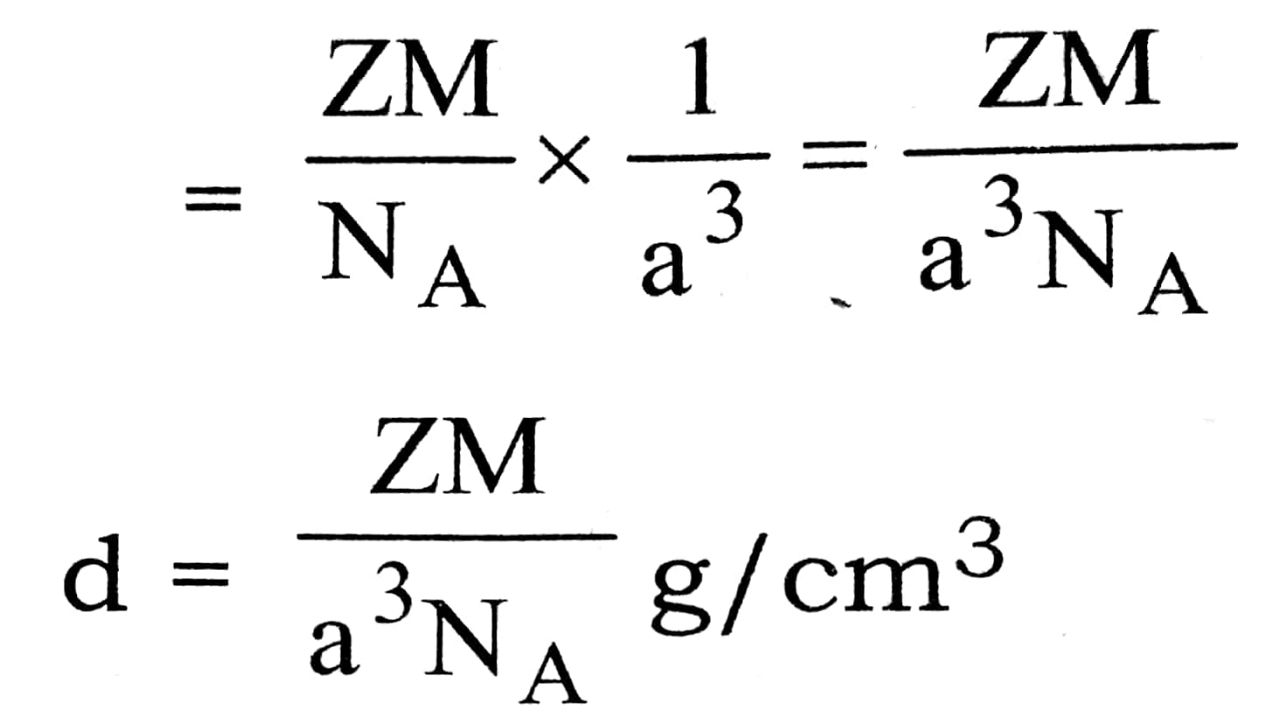
From the above expression for density, d we can calculate the atomic mass, M of metal as other parameters are known.
Q. 2. Classify each of the following as being either a p-type or an n-type semi conductor :
(i) Ge doped with In
(ii) B doped with Si.
Ans ⇒ (i) Ge is an element of 14th group (like Si) and has configuration 4s2 – 4p2. It has been doped with In, a 13th group element having 5s2 5p1 configuration i.e., element of 14th group has been doped with 13th group element. All three valence electrons of impurity atom (In) gets bonded with three out of four elections of Ge and one electron of Ge remains unbonded. Conductivity is due to unbonded electron of inslulator, Ge. Therefore, it is a p-type semi-conductor.
(ii) Boron, B is an element of 13th group and has 2s22pl configuration. It is doped with Si, an element of 14th group having 352 3p2 configuration. All three electrons of boron gets bonded with 3 out of 4 electrons of Si and 4th electron of impurity atom (i.e. Si) is responsible for conductivity. Thus it is a n-type semiconductor
Q. 3. How will you distinguish between the following pairs of terms:
(i) Hexagonal close packing and cubic close packing.
(ii) Crystal lattice and unit cell.
(iii) Tetrahedral void and octahedral void
Ans ⇒ (i) Hexagonal close packing follws AB AB AB type arrangement i.e., third layer duplicated first one and fourth layer duplicates second one. In cubic close packing ABC ABC …. type arrangement is present i.e., third layer lie in the depression of second layer that do not the directly over the atom of first layer.
(ii) Regular three dimensional arrangement points in space is known as space lattice when these points are replaced with actual atoms or ions is known as crystal lattice. On the other hand smaller portion of space lattice which can generate the complete lattice by repeating its own dimensions in various directions is known as unit cell.

(a) Octahedral void (b) Tetrahedral void
(iii) The void created by six spheres in contact is called an octahedral void Fig. (a) and void created by the four spheres in contact is called a tetrahedral void Fig. (b).
Q. 4. Explain the following with suitable examples :
(a) Paramagnetism
(b) Diamagnetism
(c) Ferromagnetism
(d) Antiferromagnetism
(e) Ferrimagnetism
(f) Piezoelectric effect.
Ans ⇒ (a) Paramagnetism : The substances which are weakly attracted by a magnetic field are called paramagnetic substances and the property of the substances is called paramagnetism. Paramagnetism is due to presence of one or more unpaired electrons which are attracted by magnetic field.
Example : O2, Cu2+, Fe3+, Cr3+ etc.
(b) Diamagnetism : Diamagnetic substances are weakly repelled by a magnetic field. H2O, NaCl and C6H6 are some examples of such substances. They are weakly magnetised in a magnetic field in opposite direction. Diamagnetism is shown by those substances in which all the electrons are paired and there are no unpaired electrons. Pairing of electrons cancels their magnetic moments and they lose their magnetic character.
(c) Ferromagnetism : A few substances like iron,cobalt, nickel, godolinium’ and CrO2 are attracted very strongly by a magnetic field. Such substances are called ferromagnetic substances. Besides strong attractions, these substances can be permanently magnetised. In solid state, the metal ions of ferromagnetic substances are grouped together into small regions called domains. Thus, each domain acts as a tiny magnet.
Example :Iron, Cobalt, Nickel etc.
(d) Antiferromagnetism : Substances like MnO showing Anti ferromagnetism have domain structure similar to ferromagnetic substance, but their domains are oppositely oriented and cancel out each other’s magnetic moment.
(e) Ferrimagnetism : This magnetic property is caused by particles on inter-penetratiaties lattices with unequal number of electrons with parallel and antiparallel spins so that there dipolemoment. FeOFe2O3 = (Fe3O4) is an example of ferrimagnetic materials.
(f) Piezoelectric effect (or pressure electricity) : Insulators do not conduct electricity be the electrons present in them are held tightly to the individual atoms or ions and do not move. However, when an electric field is applied polarisation takes place and newly formed dipoles may align themselves in an ordered manner so that such crystals have a net moment.
When mechanical stress is applied on a polar crystals so as to deform them, electricity produced due to displacement of ions. This is known as piezoelectric effect and electric so this produced is known as Piezo electricity or pressure electricity.
Exampled are : titanium, barium and led, lead zirconate (PbZrO3), ammonium dihydrogen phosphate and quartz.
Q. 5. Calculate the atomic radius in Sc, bcc and fcc crystal.
Ans ⇒ Atomic radius (r) in sc : 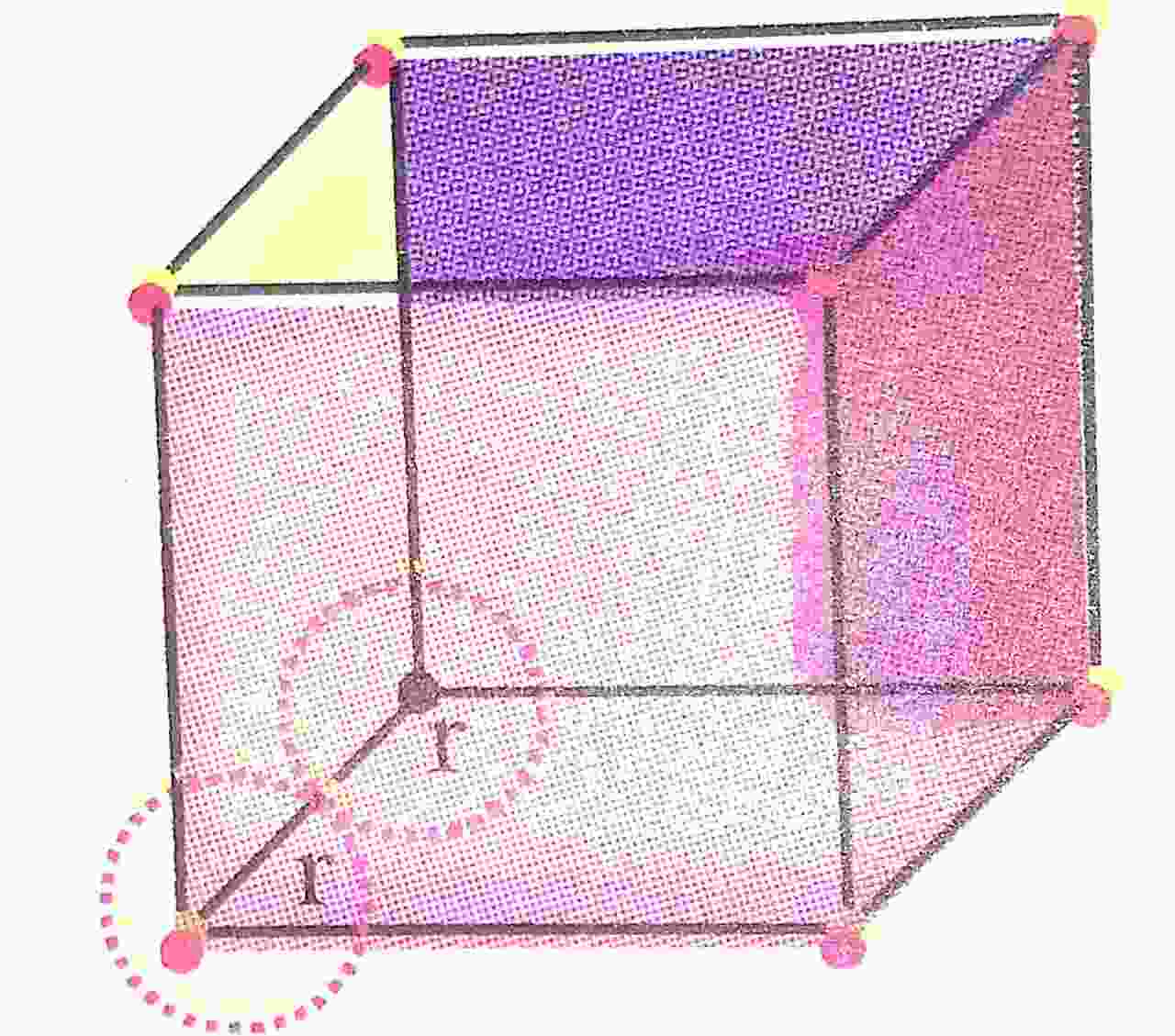
Let edge length = a
From geometry, r + r = a or, 2r = a
∴ ![]()
Atomic radius (r) in sc :
From geometry,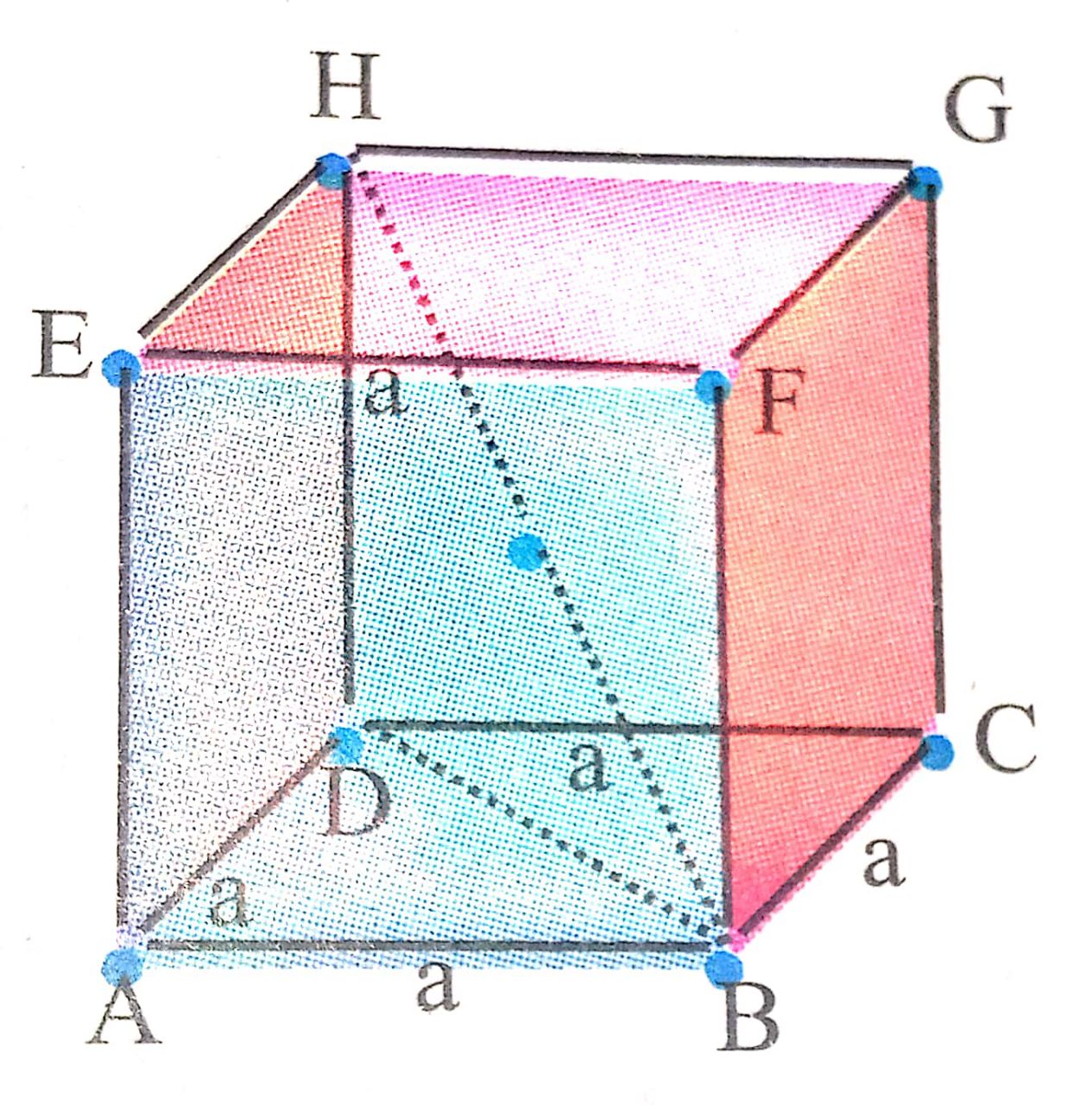
In Δ BDH
(BH)2 = (BD)2 + (HD)2
(BH)2 = (BD)2 + a2
(4r)2 = (BD)2 + a2
16r2 = BD2 + a2 ….(i)
Now from Δ BAD
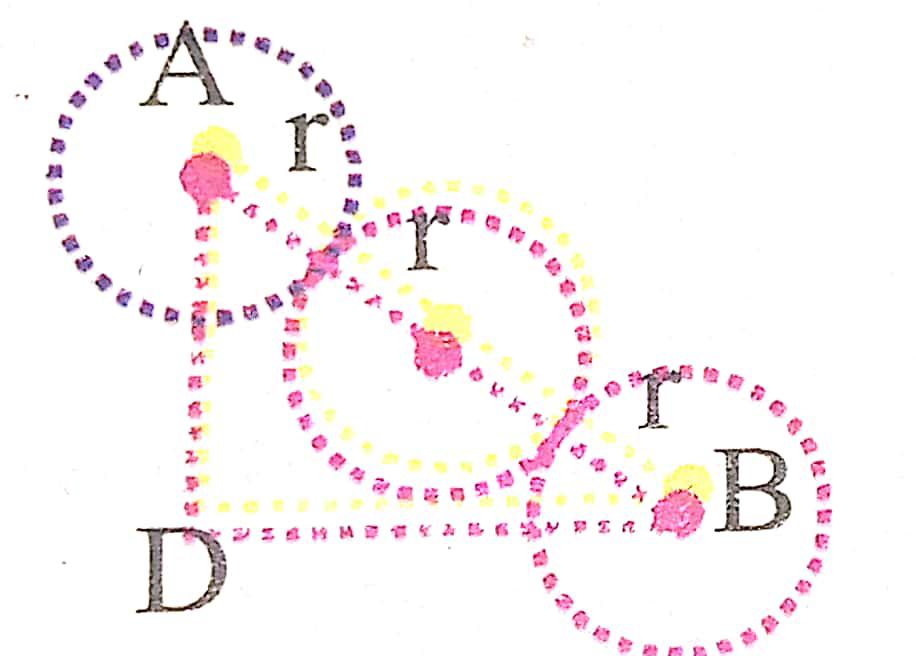
(BD)2 = (AD)2 + (AB)2
(BD)2 = a2 + a2 = 2a2… (ii)
Putting the value of (BD)2 in eq. (i)
16r2 = 2a2 + a2
![]()
Atomic radius in fcc :
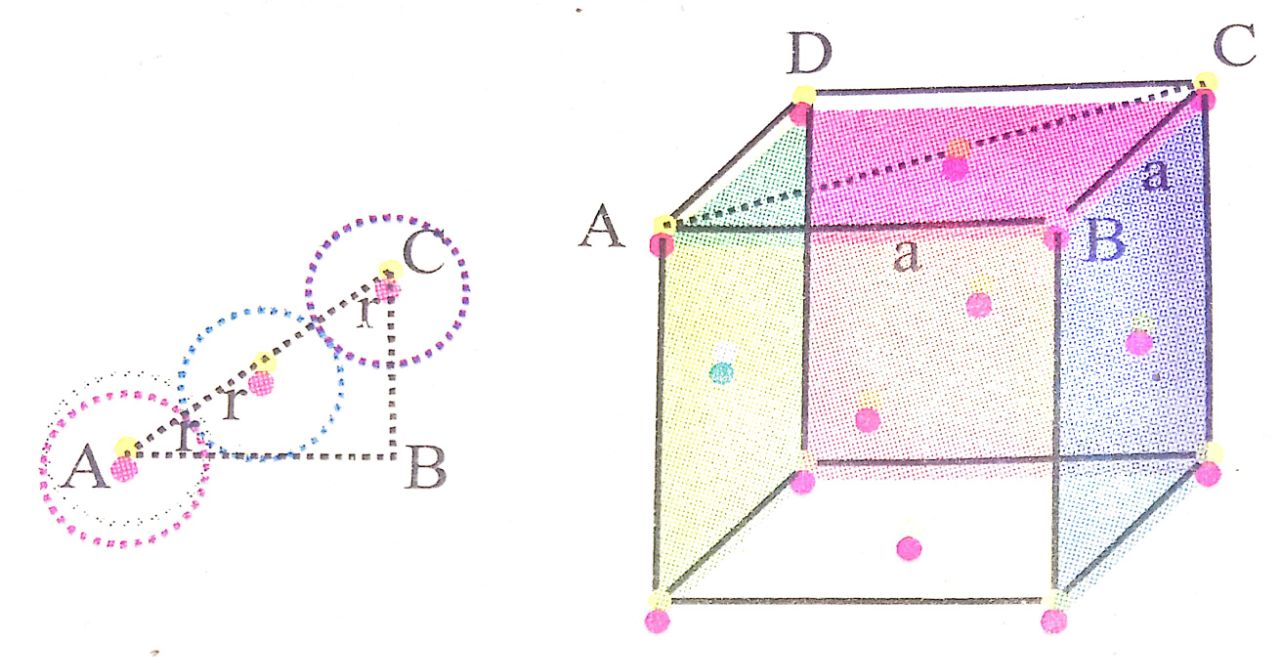
From geometry
In Δ ABC
(AC)2 = (AB)2 + (BC)2
(4r2) = a2 + a2 or , 16r2 = 2a2
![]()
Q. 6. Explain : (a) The basis of similarities and differences between metallic and ionic crystals
(b) Ionic solids are hard and brittle.
Ans ⇒ (a) Basis of Similarities : (i) Both ionic and metallic crystals have electrostatic forces of attraction In ionic crystals these are between the oppositely charged ions. In metals, these are among the valence electrons whieh are mobile or delocalised and the fixed kernels which are positively charged. That is why both have high melting points.
(ii) In both cases the bond is non-directional.
Basis of differences : (i) In ionic crystals, the ions are not free to move. Hence they cannot conduct electricity in the solid state. They can do so only in the molten or aqueous state when they become free to move. In metals, the valence electrons being MOBILE/ DELOCALIZED are free to move/flow. Hence they can conduct electricity in the solid state. Ions carry electricity in ionic crystals when present in the molten or aqueous state and mobile electrons carry electricity in metallic crystals.
(ii) Ionic bond is a strong bond, whereas metallic bond is a weak bond.
(b) Ionic crystals are hard, because there are strong electrostatic froces of attraction among the oppositively charged ions. They are brittle because ionic bonds are non-directional.
Q. 7. Classify the following solids in different categories based on the nature of intermolecular forces operating is them: Potassium sulphate, tin, benzene, urea, ammonia, water, zinc sulphide, graphite, rubidium, argon, silicon carbide.
Ans ⇒ Potassium sulphate : Ionic solid; coulombic forces of attraction.
Tin : Metallic solid; metallic bonding
Benzene (solid) : Molecular solid; dispersion or London forces.
Urea : Molecular solid, dipole-dipole attractions.
Ammonia : Molecular solid (polar) Hydrogen bonding.
Water (ice) : Molecular solid; hydrogen-bonding.
Zinc sulphide : Ionic solid, coulombic forces of attraction.
Graphite : Net-work or covalent, covalent bonds.
Rubidium: Metallic solid, metallic bonds (attraction between positive metal ions called kernels and mobile electrons)
Argon : Molecular solid, van der Waals forces.
Silicon Carbide (Sic) : Network or covalent solid. covalent bonds.
Q. 8. Analysis shows that nickel oxide has formula Ni 0.98 O1.00: What fractions of Nickel exist as Ni2+ and Ni3+ ions ?
Ans ⇒ Ni0.98 01.00 is non-stoichiometric compound and is a mixture of Ni2+ and Ni3+ ions. Let x atoms of Ni3+ are present in the compound. This means that a Ni2+ have been replaced by Ni3+ ions.
Therefore, no. of Ni2+ ions = (0.98 – x).
For electrical neutrality, positive charge on compound = negative charge on compound.
Therefore, 2 (0.98 – x) + 3x = 2
1.96 – 2x + 3x = 2
or, x = 2 – 1.96 = 0.4
Hence, % of Ni ions = ![]() × 100 = 4.08%
× 100 = 4.08%
Thus, Ni2 + is 96% and Ni3+ is 4% in given sample of nickel oxide having formula, Ni0.98 O 1.00.




